Elementary discrete mathematics

Problems

These problems correspond to the chapters of the book. Many of them are assigned homework for the class MATH 174 at Coastal Carolina University. After reading each chapter, try the problems.

If a problem is difficult to solve because you must answer in the abstract, do a few examples first to try to get a handle on the problem.

1. Sets
2. Propositional logic
3. Predicate logic
4. Proofs
5. Recursion and integer representation
6. Sequences and sums
7. Asymptotics
8. Proof by induction
9. Introduction to combinatorics
10. Ordered samples
11. Unordered samples
12. Multinomial coefficients
13. Probability
14. Boolean matrices
15. Relations
16. Closure and composition
17. Equivalence relations
18. Partial orders

1. Sets

Write the following sets in roster notation. If there are more than ten elements in the set, you may use ellipses (…) once the pattern is clear and you have written down four elements.
a) Prime numbers less than (but not equal to) 10
b) The letters in the alphabet
c) The set of positive odd integers
d) Teams in the NBA Southeast Division
Write the following sets in set-builder notation.
a) $\{0,1,2,3,4,5,6,7,8,9\}$
b) $\{2,3,5,7,11,13,17,19\}$
c) $\{\varnothing, \{a\}, \{b\}, \{a,b\}\}$
Calculate the power set of $X=\{1,2,3\}$ .
Calculate the power set of $X=\{1,2,3,4\}$ .
Given $A=\{a,b,c\}$ and $B=\{c,d,e\}$ , compute the following. If the answer is a set, answer in list/roster notation.
a) $A \cup B$
b) $A \cap B$
c) $A-B$
d) $B-A$
e) $B \times A$
f) $\mathcal{P}(A)$
g) $|A|$
h) $|A \cup B|$
i) $|\mathcal{P}(B)|$
Let $X=\{1,3,5\}$ , $Y=\{2,4,6\}$ , and $Z=\{2,3,5\}$ . consider the universal set to be $\Omega=\{1,2,3,4,5,6\}$ . Compute the following. If the answer is a set, answer in list/roster notation.
a) $X \cup Y$
b) $X \cap Z$
c) $Y \cap X$
d) $|X \cup Z|$
e) $\overline{Z}$
f) $X \times Z$
g) $X \cup (Y \cap Z)$
h) $\mathcal{P}(Z)$
i) $|Y\times Z|$
Compute each of the following given that the universal set is $\Omega=\{0,1,2,3,4,5,6,7,8,9\}$ .
a) $\{1,2,5\} \cup \{2,5,8,9\}$
b) $\overline{\{2,3,7\}}$
c) $\{x \in \Omega \; | \; x \text{ is odd}\} \cap \{0,3,4,9\}$
d) $|\{0,1\} \times \Omega|$
e) $\mathcal{P}(\mathcal{P}(\{0,1\}))$
Let the universal set be that of people reading this book. Let $X$ be the set of people studying mathematics, and $Y$ be the set of people studying computer science. To which of the following sets do you belong: $X$ , $Y$ , $X \cup Y$ , $X \cap Y$ , $\overline{X}$ , and/or $\overline{Y}$ ?
Tell whether each of the following statements are true or false.
a) $3 \in \mathbf{Z}$
b) $-1 \not\in \mathbf{Z} - \mathbf{N}$
c) $0 \in \mathbf{Z}-\mathbf{N}$
d) $\mathbf{Z} \subseteq \mathbf{N}$
e) $\mathbf{N} \cup \mathbf{Z} = \mathbf{Z}$
f) $\mathbf{N} \cap \mathbf{Z} = \mathbf{Z}$
Tell whether each statement is true or false if $A=\{a,b\}.$
a) $a \in \mathcal{P}(A)$
b) $\{a\} \in \mathcal{P}(A)$
c) $\{\{a\}\} \in \mathcal{P}(A)$
d) $\{\{a\}\} \subseteq \mathcal{P}(A)$
Suppose that $X$ , $Y$ , and $Z$ are finite sets. Give a formula for $|X \cup Y \cup Z|$ (the cardinality of the set of all elements in at least one of $X$ , $Y$ , or $Z$ ) reminiscent of the formula for $|X \cup Y|$ .
Often, $[n]$ is used to denote the set $\{1,2,\ldots, n\}$ , the set of positive integers at most $n$ .
a) What is $\displaystyle \bigcup_{n \ge 1} [n]$ ? (The union is taken over all positive integers $n$ .)
b) What is $\displaystyle \bigcap_{n \ge 1} [n]$ ? (The union is taken over all positive integers $n$ .)

2. Propositional logic

Consider the sentence “Bob is wearing flip flops or it is cold out.”
a) Choosing your own letters, symbolize this statement. (Hint: In the northern United States there is an unspoken but universally acknowledged competition to be the last man in shorts and flip-flops.)
b) Write a truth table for this statement.
Let $p$ stand for “I attended class” and $q$ stand for “I did the homework.”
a) Symbolize “I attended class but I did not do the homework.” (Hint: In English, the word “but” suggests that two statements, maybe surprisingly, are simultaneously true.)
b) Write a truth table for this statement.
Let $p$ stand for “I attended class,” $q$ stand for “I did the homework,” and let $r$ stand for “I failed the exam.” Consider the statement “If I attended class but did not do the homework, then I failed the exam.” Should it be symbolized as $(p \wedge \neg q) \to r$ or $p \wedge (\neg q \to r)$ ? Write a truth table for each and decide which best captures the meaning of the English statement.
Tell whether the statement “Alicia is doing homework or she is playing video games” is an inclusive disjunction $\vee$ or an exclusive disjunction $\oplus$ .
Write a truth table for $s \leftrightarrow \neg(t \wedge u \wedge \neg v)$ .
Is $[(p \to q) \wedge q]\to p$ a rule of inference?
Suppose that if it rains, then I bring my umbrella. Can you conclude whether it is raining (and explain why) if
a) I did bring my umbrella?
b) I did not bring my umbrella?
Which of the following are equivalent?
a) $p \to q$
b) its converse, $q \to p$
c) its contrapositive, $\neg q \to \neg p$
d) its inverse, $\neg p \to \neg q$
Show that $(p \wedge q) \to (p \vee q)$ is a tautology
a) with a truth table.
b) algebraically. (To do this, apply valid equivalences until you arrive at $\varphi \vee \neg \varphi$ , which is equivalent to $T$ by $\vee$ -cancellation, for some statement $\varphi$ .)
Show that $(p \leftrightarrow q) \equiv (\neg p \leftrightarrow \neg q)$
a) with a truth table.
b) algebraically.
Show that $[(p \to s) \wedge (q \to s) \wedge (r \to s)] \to [(p \vee q \vee r) \to s]$ is a rule of inference
a) with a truth table.
b) algebraically.
(This generalizes to the technique proof by cases, which proves $(p_1 \vee p_2 \vee \cdots \vee p_n) \to q$ by showing that $p_i \to q$ is true for all $i = 1, 2, \ldots, n$ .)

3. Predicate logic

For Problems 3.1-3.4, let $C(x)$ stand for " $x$ is a cloobledoo,’’ $G(x)$ stand for " $x$ is green,’’ $H(x,y)$ stand for " $x$ hunts $y$ ,’’ and $Q(x)$ stand for " $x$ is a quarpake.’’ (You are not supposed to know what a cloobledoo or what a quarpake – pronounced “kwar-puh-kee” – are, but you are encouraged to doodle what you think each looks like.)

Symbolize each of the following sentences.
a) There is something that is green but not a cloobledoo.
b) Every green quarpake is a cloobledoo.
c) Every cloobledoo is a quarpake, but not all quarpakes are cloobledoos.
Consider the statement $\forall x [C(x) \to G(x)]$ .
a) Translate this statement into words.
b) Give an example of a situation in which this statement is false.
c) Symbolize the negation of this statement where no negation ( $\neg$ ) appears to the left of a quantifier ( $\forall$ or $\exists$ ).
d) Translate the negation of the statement into words.
Consider the statement $\forall x \exists y [(Q(x) \to (C(y) \wedge H(x,y))]$ .
a) Translate this statement into words.
b) Give an example of a situation in which this statement is false.
c) Symbolize the negation of this statement where no negation appears to the left of a quantifier.
d) Translate the negation of the statement into words.
Consider the statement $\exists x \forall y [Q(x) \wedge (H(x,y) \leftrightarrow G(y))]$ .
a) Translate this statement into words.
b) Give an example of a situation in which this statement is false.
c) Symbolize the negation of this statement where no negation appears to the left of a quantifier.
d) Translate the negation of the statement into words.

For problems 3.5-3.8, let $C(x)$ be " $x$ is continuous,’’ $D(x)$ be " $x$ is differentiable,’’ $E(x,y)$ be " $x$ and $y$ are equal.’’ These predicates are defined on the space of all functions to and from the real numbers and $f$ is the name of a known function.

Symbolize "Every differentiable function is continuous.’’
Translate $\exists xy [E(x,y) \to (C(x) \wedge \neg C(y))]$ into English.
Symbolize the negation of $\exists x \forall y \exists z (E(y,z) \wedge C(x))$ such that no negation appears to the left of a quantifier.
Translate $\Big( \forall xy [(E(x,y) \wedge C(x)) \to C(y)] \wedge \exists y [E(f,y) \wedge C(y)]\Big) \to C(f)$ into English.
Remember when we proved that the empty set was a subset of any set and you were told to just go with it for the time being? Now we will fully justify ourselves.
a) Prove that $\forall x[P(x) \to Q(x)]$ and $\neg \exists x[P(x) \wedge \neg Q(x)]$ are equivalent.
b) Explain how this proves that the empty set is a subset of any other set. In particular, tell what the predicates $P$ and $Q$ are in this context.

4. Proofs

Let $n$ be an integer. Prove that if $n$ is even, then $n^2+2n+3$ is odd.
Prove that if $2n^2+7n$ is even and $n$ is an integer, then $n$ is even.
Let $n$ be an integer. Prove that $n$ is odd if and only if $3n^2-7$ is even.
Prove that $n^2-n$ is even for any integer $n$ . (Hint: There are two ways you could approach this proof. Here’s a hint for each: I. The integer $n$ must be even or odd. Then do a proof in each case. This is an example of proof by cases, which you established was valid in the last problem set. II. You could do something to $n^2-n$ that makes this fact obvious.)
Prove that the sum of two integers is odd if and only if one is even and the other is odd. (Hint: The first line of one direction of the proof is “Let $m$ and $n$ be integers…”)
Let $(a,b,c)$ be a Pythagorean triple, i.e. three positive integers satisfying the Pythagorean theorem $a^2+b^2=c^2$ . Prove both $a$ and $b$ cannot be odd.
Prove that if 3 divides $n$ , then 3 divides $n^2+2n+6$ .
Prove that if 4 divides $n$ , then 8 divides $2n^2 + n^3$ .
Prove that if $n^2+3$ is divisible by 3 then $n$ is divisible by 3. (Hint: if $n$ is not divisible by $3$ , then $n$ has the form $3k+1$ or $3k+2$ for some integer $k$ . Do a proof for each.)
Prove that $a|a$ for all nonzero integers $a$ .
Prove that if there exist nonzero integers $a$ , $b$ , and $c$ such that $a|b$ and $b|c$ then $a|c$ .

In the remaining problems, remember the following definitions:

$X \subseteq Y$ if for all $x \in X$ , also $x \in Y$ .
$X = Y$ if for all $x \in X$ then $x \in Y$ , and for all $y \in Y$ then $y \in X$ .
$x \in X \cup Y$ means $x \in X$ or $x \in Y$ .
$x \in X \cap Y$ means $x \in X$ and $x \in Y$ .
$x \in \overline{X}$ means $x$ is not in $X$ .

Prove the theorem of equality by mutual inclusion: Let $X$ and $Y$ be sets. Then, $X=Y$ if and only if $X \subseteq Y$ and $Y \subseteq X$ .
Prove DeMorgan’s law for unions: $\overline{X \cup Y} = \overline{X} \cap \overline{Y}$ .
Prove DeMorgan’s law for intersections: $\overline{X \cap Y} = \overline{X} \cup \overline{Y}$ .

5. Recursion and integer representation

Give an example of recursion not found in the chapter.
Write $2,391$ in
a) binary.
b) octal.
c) hexadecimal.
Write $(11010101)_2$
a) decimal.
b) octal.
c) hexadecimal.
Write $(AF3)_{16}$ in
a) decimal.
b) binary.
c) octal.
Compute the following numbers in the given bases.
a) $2,043$ in binary
b) $(11010110)_2$ in decimal
c) $2,043$ in hexadecimal
Use binary numbers to prove that $1 + 2 + 2^2 + 2^3 + \cdots + 2^n = 2^{n+1}-1.$
A number written in ternary is written in base-3 with digits 0, 1, and 2. Write the number 115 in ternary.
Write the number 115 in base-9.

6. Sequences and sums

Let $(a_n)$ be a sequence defined by $a_n = 2^n - 1$ . Calculate $a_5$ .
Write down the first six terms of the sequence $(x_n)$ given by $x_n=2n-3$ where $n \ge 0$ .
Let $(y_n)$ be the sequence given by the relation $y_n = 3y_{n-1} + 2$ where $y_0=0$ . Calculate $y_5$
a) iteratively.
b) recursively.
Let $(b_n)$ be a sequence defined by $b_n = \begin{cases} 4b_{n-2} - b_{n-1} & n \ge 2 \\ 3 & n=1 \\ -1 & n=0 \end{cases}$
Compute $b_4$
a) iteratively.
b) recursively.
Consider the sequence $(x_i)$ whose terms are given by the following recurrence relation: $x_i = \begin{cases} ix_{i-1} - 2x_{i-2} & i \ge 2 \\ 1 & i = 1 \\ 1 & i = 0 \end{cases}$
a) Calculate $x_4$ iteratively.
b) Calculate $x_4$ recursively.
Let $(z_n)$ be the sequence given by the relation $z_n=z_{n-1}z_{n-2}$ where $z_0=2$ and $z_1=3$ . Calculate $z_5$
a) iteratively.
b) recursively.
Calculate $\displaystyle \sum_{n=2}^5 n^2$ .
Calculate $\displaystyle \sum_{i=1}^7 (2i-1)$ .
Calculate $\displaystyle \sum_{i=1}^4 i!$ .
Calculate $\displaystyle \sum_{j=0}^3 \dfrac{j}{j+1}$ .
Calculate $\displaystyle \sum_{m=2}^4 \sum_{n=m-1}^{m+1} mn$ .
Calculate $\displaystyle \sum_{j=2}^4 \sum_{k=5}^8 (k-j)$ .
Calculate $\displaystyle \sum_{n=0}^2 \sum_{k=1}^3 k^n$ .
Let $(x_n)$ be a sequence where $\displaystyle\sum_{n=1}^{100} x_n = 50$ , and $x_{100}=12$ . Calculate $\displaystyle \sum_{n=1}^{99} 3x_{n}$ .
Suppose that $\displaystyle \sum_{m=5}^{904} c_m = 1,307$ , $c_4=42$ , and $c_{904}=10$ . Compute $\displaystyle \sum_{m=4}^{903} 3c_m.$
Given that $\displaystyle \sum_{n=0}^{100} x_n = 471$ , $\displaystyle \sum_{n=0}^{99} y_n = 502$ , $x_{100}=30$ , and $y_{100}=12$ , calculate
a) $\displaystyle \sum_{n=0}^{100} y_n$ .
b) $\displaystyle \sum_{n=0}^{99} (3x_n - y_n)$ .

7. Asymptotics

In some of the following problems, you must arrange functions by growth rate. Note sometimes two functions are big- $O$ of one another. In that case, those two functions may go in any order.

Arrange the following functions in ascending order of growth rate: $n^2, \log n, n!, n \log n, n^3, 1, n.$
Arrange the following functions in ascending order of growth rate: $2n+1$ , $n^2+n$ , $2^n \log n$ , $2^n+100n$ , $n^2\log n$ , $503$ .
Arrange the following functions in ascending order of growth rate: $4000\log n$ , $2n^2+13n-8$ , $1,036$ , $3n \log n$ , $2^n-n^2$ , $2n!-n$ , $n^2-4n$ .
Give the simplest function $b_n$ of lowest order such that $4n^3+3n^2 \log n=O(b_n)$ .
Give the simplest function $b_n$ of lowest order such that $(8n^3 + 20n)(2^n + 4\log n)=O(b_n)$ .
Let $a_n = n^3 + n^6 + 8n^5\log n$ . Give the simplest function $b_n$ of lowest order where $a_n=O(b_n)$ .
Suppose that $a_n= (8n+n^2)(5n+\log n+n \log n)(3n-8n^5+n!)$ . Give the simplest function $b_n$ of lowest order where $a_n=O(b_n)$ .
Suppose that $a_n = (2+n^3)(2^n + 5n)$ . Choose the function $b_n$ that grows the most like $a_n$ . (In other words, $a_n$ and $b_n$ should be big-O of each other.)
a) $b_n = 5n + 2^n + 7$
b) $b_n = 10n + n\log n + 1$
c) $b_n = 256n^3 \cdot 2^n - \log n$
d) $b_n = n! + 8n - 1$
It turns out that $n^2+3n+1$ is big- $O$ of $n^2$ . This means that there exist integers $k$ and $C$ where for all $n \ge k$ , $n^2+3n+1 \le Cn^2$ . Find values for $k$ and $C$ that work. You may use this Desmos applet to choose a value of $C$ so that $n^2+3n+1 \le Cn^2$ .

8. Proof by induction

Prove by induction that $\sum_{m=1}^n (2m-1) = n^2$ for any $n \ge 1.$
Prove by induction that if $n \ge 1$ , then $\sum_{i=1}^n i^2 = \dfrac{n(n+1)(2n+1)}{6}.$
Prove by induction that for $r\neq 1$ , if $n \ge 0$ , then
$\sum_{i=0}^n r^i = \dfrac{r^{n+1}-1}{r-1}.$
Prove $6$ divides $7^n-1$ for all $n \ge 1$ .
Prove $4$ divides $9^n + 11$ for all $n \ge 1$ .
In one proof, prove that $3$ and $5$ both divide $16^n + 14$ for all $n \ge 1$ . (Hint: If $3$ and $5$ both divide a number, then so does…)
Prove by induction that if $n \ge 6$ , then $n^2+5n+1 \le 2n^2$ .
Prove by induction that $n^2+7n+3 \le 3n^2$ for $n \ge 4$ .
Prove by induction that if $n \ge 35$ , then $n^2+100n+100 \le 4n^2-1$ .
Prove by induction that $2n+1 \le 2^n$ for all $n \ge 4$ .
Prove by induction that $n^2 \le 2^n$ for all $n \ge 4$ . (Hint: Use the preceding problem.)
Prove by induction that $n^3+3n+1 \le 2n^3$ for all $n \ge 2$ . (Hint: You will learn soon that $(k+1)^3 = k^3+3k^2+3k+1$ .)
Prove by induction that a set with $n$ elements has $2^n$ subsets for all $n \ge 0$ .
Prove that $3n^2+8n+1=O(n^2)$ from the definition of big- $O$ . (Hint: You must find your own values of the threshold and the constant multiple.)

9. Introduction to combinatorics

Alex is choosing a class to take next semester. They can choose from $9$ math classes or $7$ computer science classes, of which $3$ are cross-listed (listed as both math and CS courses). How many classes can they choose from?
Enumerate all possible ways there are to choose two elements from the set $\{a,b,c,d,e\}$ if:
a) you can choose the same element twice and the order of the elements chosen matters?
b) you can choose the same element twice and the order of the elements chosen does not matter?
c) you cannot choose the same element twice and the order of the elements chosen matters?
d) you cannot choose the same element twice and the order of the elements chosen does not matter?
A math teacher has access to a textbook that includes $60$ questions. Of these $60$ questions all are at least easy or important, $42$ are easy, and $23$ are important. How many questions are both easy and important?
[rewritten SP21] Your math professor has 17 books with yellow covers and 5 books with green covers. How many ways can they choose two books for a course, where one has a yellow cover and one has a green cover? (Most math books bear a single color.)
Two distinguishable six-sided dice are rolled (e.g., one is red and one is blue) and the sum of both rolls is tallied.
a) How many possible outcomes are there? (Hint: List them in a grid.)
b) How many ways are there for the sum of the two rolls to be at least (including) $7$ ?
c) How many ways are there to get a prime sum?
d) How many ways are there to get a sum that is prime or at least $7$ ?
e) Each die is rolled separately, one at a time. How many ways can the first roll be odd and the second roll be prime?
In a 64-team single-elimination tournament, how many games are played? (“Single-elimination” means that a team is out of the tournament upon losing once. The winner is the only team that never loses.) Once you have solved the problem using the tools from this chapter, see if you can think of a more clever approach. This problem was stolen with permission from Jay Cummings’ book Real Analysis: A Long-Form Mathematics Textbook, where I saw it first.
Prove that a set with $n$ elements has $2^n$ subsets.

10. Ordered samples

There are ten volunteers to form a team of four people where everyone on the team has a different role. How many such teams are possible?
A case-sensitive alphanumeric password is a password whose characters may be the capital letters A through Z, the lowercase letters a through z, and the digits 0 through 9. How many case-sensitive alphanumeric passwords with $n$ characters are there?
A 10-character case-sensitive alphanumeric password is to have no repeated characters. How many such passwords are there?
A 10-character case-sensitive alphanumeric password is to be made with at least one repeated character. How many such passwords are there? (Hint: Last two questions.)
A 10-character case-sensitive alphanumeric password is to be made so that it is a palindrome; that is, the last half of the password is just the first half in reverse. How many of these passwords are there?
Recall that the set $X \times X$ is the set of all ordered pairs $(x,y)$ where both $x$ and $y$ are elements of $X$ . (a) If $X$ has $n$ elements then how many elements of $X \times X$ are there? (b) How many subsets does $X \times X$ have?
The \textbf{diagonal} is the subset of $X \times X$ consisting of all pairs of the form $(x,x)$ —in other words, those pairs whose first and second elements are the same.
(a) How many elements are on the diagonal of $X \times X$ if $|X|=n$ ?
(b) In that case, how many ordered pairs are “off the diagonal”?
How many ways can four couples sit in a row such that everyone sits next to their partner?
How many ways can nine different people be seated in a circle?

11. Unordered samples

(a) How many ways are there to flip five coins and get three heads?
(b) How many binary strings with five digits have exactly three 1’s?
(c) How many subsets of the set $\{a,b,c,d,e\}$ have three elements?
How many ways are there to flip seven coins and get at least five heads?
A seven-game series between the Toronto Raptors and the Golden State Warriors ends as soon as one team wins four games. How many ways can the series go? (In other words, you are counting strings of the form “TTTGGGT” or “TGGGG” where T or G appears exactly four times.)
A research team is to be made in the following way. There are two professors on the team, one of whom is the principal investigator. There are five students on the team who all have the same job. If eight professors and ten students volunteer, how many such teams are possible?
How many ways can fifteen people be divided into four teams if all that matters is how many people are on each team?
How many non-negative integer solutions are there to the equation $w+x+y+z=58$ ?
Goofus and Gallant are going to the ice cream parlor. The parlor has $31$ flavors. Goofus and Gallant will each get three scoops on a cone.
(a) Goofus, the absolute rube, doesn’t care what order his scoops are in. How many ways can he make his cone?
(b) Gallant, a man of taste, cares what order his scoops are in. How many ways can Gallant make his cone?
Goofus has $10 to bet that a particular team will win the NBA finals. He can bet on the Bucks, the Raptors, the Warriors, or the Nuggets. Goofus can place his bets in one-dollar increments (he may bet $0 or $1 on a team, but not $0.50). How many ways can Goofus allocate his money? (Gallant does not gamble.)
How many ways can twenty wedding guests be seated at five tables if each table has unlimited capacity, and all that matters is how many people are at each table?
Let $\Omega=\{x,y,z\}$ .
(a) Enumerate all the multisets from $\Omega$ of cardinality $r=3$ .
(b) How many \textit{distinguishable} terms are in the polynomial $(x+y+z)^3$ ?
Write and simplify the binomial $(x+y)^{10}$ in expanded form.
Write and simplify the binomial $(3m-n)^5$ in expanded form.
Use the binomial theorem to prove that if $n \ge 1$ , $\sum_{r=0}^n (-1)^r\binom{n}{r} = 0.$
Fix $n \ge 1$ . Let $E$ be the sum of all the $C(n,r)$ where $r$ is even, and let $O$ be the same sum where $r$ is odd. Which is larger: $E$ or $O$ ? (Hint: Last question.)
Use algebra to prove the binomial coefficient recurrence relation. That is, prove it just using the factorial definition of the binomial coefficient. Do not appeal to what the coefficients are counting.
Use a combinatorial proof to prove that $\sum_{r=0}^n \binom{n}{r} = 2^n.$ In other words, what sort of object is each side of the equation counting?
Generating functions allow us to use tools from algebra, calculus, and elsewhere to learn about sequences. Differentiating both sides of the binomial theorem with respect to $y$ yields the identity $n(x+y)^{n-1} = \sum_{r=0}^n r\binom{n}{r}x^{n-r}y^{r-1}.$
(a) If you have had calculus, verify this yourself.
(b) Calculate the value of the sum $\sum_{r=0}^n r\binom{n}{r}.$
A monic polynomial is a polynomial whose leading term is 1, e.g. $p(z)=z^3-2z+7$ . Monic polynomials are uniquely determined by their roots, i.e. values $z=c$ where $p(c)=0$ , and the multiplicity of each root, i.e. the number of times $p(z)$ is divisible by $(z-c)$ . The degree of a polynomial is the sum of the multiplicities of each root. Anyway, count the number of monic polynomials of degree 5 whose roots are one of the first ten natural numbers, i.e. elements of $\{0,1,2,3,4,5,6,7,8,9\}$ . (Hint: Where have you seen the word “multiplicity” before very recently?)

12. Multinomial coefficients

How many different teams can be made if we must make $8$ teams from $30$ people where the first four teams each have $4$ people, the fifth has $3$ people, the sixth has $2$ people, and the seventh has $3$ people?
Five students are to be allocated into three distinguishable teams.
(a) How many distributions are there? In other words how many different possible sizes can the teams have? (Include empty teams.) e.g. “Team 1 and 2 each have two members and Team 3 has one member” is one of the distributions being counted; perhaps $221$ is a good way to represent this distribution. Enumerate all possible distributions and then check your answer with the appropriate formula.
(b) Suppose a distribution is chosen: two students will be on the first and second teams each, while a single student will be on the third team. How many different combinations of teams are there? e.g. “Team 1: Alicia and Carlos, Team 2: Davina and Bob, Team 3: Erik” is one of the combinations of teams being counted. Perhaps $AC|DB|E$ is a good way to represent these teams. Enumerate all possible combinations of teams and check your answer with the appropriate formula.
A lazy math teacher is writing an exam.
(a) The lazy math teacher has a class of 31 students and wants to assign some of them A’s, some B’s, some C’s, some D’s, and some F’s. If it is not important to the teacher how many of each grade is assigned, how many ways can they choose how many of each to give?
(b) The lazy math teacher has a class of 31 students and wants to assign 3 A’s, 6 B’s, 10 C’s, 6 D’s, and the rest F’s. It is not important to the teacher which student gets which grade. How many ways can this assignment be done?
How many distinguishable arrangements are there of the letters in ANTIDISESTABLISHMENTARIANISM?
What is the coefficient of the term $w^3x^4yz$ in the polynomial $(w+x+y+z)^9$ ?
Expand $(x+y+z)^2$ without the distributive property (i.e., without “FOILing”).
Calculate $\sum_{r_1+r_2+r_3=n} \binom{n}{r_1,r_2,r_3}.$ Give an explanation for your answer.
The binomial coefficients could be represented visually using a triangle, incorporating their recurrence. How can the trinomial coefficients be visually represented? Find a way to draw this object from $n=0$ down to $n=4$ . (Hint: Slices, or colored pencils.)

13. Probability

Alice has courtside tickets to see the Charlotte Hornets. She has a Muggsy Bogues bobblehead on her desk and has Kemba Walker’s jersey. (Those are, or were, Hornets players.) Which of these two events is more likely: that Alice works in real estate, or that Alice works in real estate and is a Hornets fan?
Of a particular basketball player’s shots, $60\%$ are worth 3 points. In general they make $40\%$ of their shots. Of the player’s 3-point shots, $30\%$ make it in the basket.
(a) What is the probability that a shot is worth 2 points? (Assume all shots are worth 2 or 3 points.)
(b) What is the probability that a shot is worth 3 points and makes it?
(c) What is the probability that a shot is worth 3 points or makes it?
(d) Of the shots that make it, how many are 3-point shots?
A twenty-sided die is rolled. (The sides are labeled 1-20.)
(a) What is the probability that the result is at least 6?
(b) What is the probaility that the result is prime given that it is at least 6?
(c) What is the probability that the result is at least 6 and prime? (Use both enumeration and the formula.)
(d) What is the probability that the result is at least 6 or prime? (Use both enumeration and the formula.)
What is the probability that a randomly-chosen binary string of length 10 has exactly 3 1’s?
A six-character alphanumeric password is made.
(a) What is the probability that the password contains all letters?
(b) What is the probability that the password has no repeated characters?
(c) What is the probability that the password has all letters given that it has no repeated characters?
(d) What is the probability that the password has repeated characters?
Let $\Omega$ be a finite sample space containing events $E$ and $F$ . Prove the following properties of probability using the definition.
(a) $0 \le P(E) \le 1$ for all events $E \subseteq \Omega$ .
(b) $P(E) = 0$ if and only if $E = \varnothing$ .
(c) $P(E) = 1$ if and only if $E = \Omega$ .
(d) If $E \subseteq F$ , then $P(E) \le P(F)$ .
A particular illness has an incidence rate of 0.3%, meaning that the probability anyone in the population has it is only 3 out of 1000. Suppose that in specimens containing the illness, a test gives a positive 80% of the time. Furthermore the same test has a 10% false positive rate (positive if the specimen does not contain the illness).
(a) Let $A$ be the event that an individual is sick with the illness and let $B$ be the event they test positive. Explain why $P(B) = P(B \cap A) + P(B \cap \overline{A})$ . (This is true regardless of what $A$ and $B$ are, by the way.)
(b) Calculate $P(A|B)$ , the probability that an individual is sick given they test positive.
(c) Calculate $P(A|B)/P(A)$ . This ratio represents the factor by which a belief the individual is sick, quantified by a probability, should increase given the evidence of a positive test. Bayes’ theorem (which you used unknowingly in part (b)) quantifies the way belief can change with evidence. For more, check out this article.

14. Boolean matrices

Given these matrices, answer the following questions or compute the following matrices (if they exist). $A = \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right), \qquad B = \left( \begin{array}{cc} 1 & 1 \\ 0 & 0 \\ 1 & 0 \end{array} \right),$
$C = \left( \begin{array}{cc} 1 & 0 \\ 1 & 1 \end{array} \right), \qquad \text{and} \qquad D = \left( \begin{array}{ccc} 1 & 1 & 0 \\ 0 & 1 & 0 \\ 1 & 0 & 1 \end{array} \right).$ a) Calculate $A \vee C$ .
b) Calculate $A \wedge C$ .
c) Calculate $A \wedge B$ .
d) Calculate $A \odot B$ .
e) Calculate $B \odot A$ .
f) Calculate $D \odot B$ .
g) Calculate $D^{[2]}$ (which is the same as $D \odot D$ ).
Calculate the following matrices. If a matrix does not exist, say so.
a) $\left( \begin{array}{rrr} 1 & 0 & 1 \\ 0 & 1 & 1 \end{array} \right) \vee \left( \begin{array}{rrr} 0 & 0 & 1 \\ 1 & 0 & 1 \end{array} \right)$
b) $\left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 1 & 1 \\ 0 & 0 \end{array} \right) \wedge \left( \begin{array}{cc} 0 & 0 \\ 1 & 1 \\ 0 & 1 \\ 1 & 0 \end{array} \right)$
c) $\left( \begin{array}{ccc} 0 & 1 & 1 \\ 1 & 0 & 1 \end{array} \right) \odot \left( \begin{array}{cccc} 1 & 0 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 1 & 0 & 0 & 0 \end{array} \right)$
d) $\left( \begin{array}{rrrr} 0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 1 & 1 \end{array} \right)^T$
Consider the set described at the beginning of the chapter, of all propositional statements together with their disjunctions, conjunctions, and negations. Be specific about how this set forms a Boolean algebra. What are the join, meet, and complement operations? Which object would play the role of $1$ , and which object would play the role of $0$ ?
Likewise, consider a family of sets that contains the unions, intersections, and complements of those sets. Describe how it forms a Boolean algebra: Identify the join, meet, and complement operations, which object would play the role of $1$ , and which object would play the role of $0$ .

15. Relations

Write each relation as a set of ordered pairs.
a) $R = \{(x,y) \; | \; y=x^2 \}$ on the set of integers between & including $-10$ and $10$
b) $S = \{ (m,n) \;|\; m, n \in \mathbf{Z} \text{ and } m+n=10 \}$ on the set $\{1,2,\ldots,10\}$
c) $T = \{(E,F)\;|\;E \subseteq F \subseteq X\}$ on the power set of $\{a,b\}$
d) The relation on $\{1,2,3,4,5\}$ where $x$ is related to $y$ if $x = y$
e) The relation on $\{1,2,3,4,5\}$ where $x$ is related to $y$ if $x < y$
f) The relation where $X$ is related to $Y$ if $|X|=|Y|$ on the power set of $\{a,b\}$
Given each relation write down the properties that the relation has. If the relation does not have a particular property, give an example showing why.
a) $R = \{(a,a), (a,c), (b,b), (c,b), (c,c)\}$
b) $S = \{ (m,n) \;|\; m, n \in \mathbf{Z} \text{ and } m+n=10 \}$
c) $T = \{(E,F)\;|\;E \subseteq F \subseteq X\}$
d) The relation on any set where $x$ is related to $y$ if $x=y$
e) The relation on any set of real numbers where $x$ is related to $y$ if $x<y$
f) The relation on any collection of sets where $X$ is related to $Y$ if $|X|=|Y|$
g) The relation on $\mathbf{R}$ where $x$ is related to $y$ if $y=x^2$
Let $X=\{a,b,c,d\}$ and the relation $R$ on $X$ be defined by $R = \{(a,b),(a,d),(b,d),(c,c)\}.$
a) Write down a matrix for $R$ where the rows and columns are arranged alphabetically.
b) Draw a digraph for $R$ .
Let $Y=\{a,b,c,d,e\}$ and the relation $S$ on $Y$ be defined by
$S = \{(a,b),(b,d),(c,d),(d,c),(d,e),(e,a)\}.$
a) Write down a matrix for $S$ where the rows and columns are arranged alphabetically.
b) Draw a digraph for $S$ .
Let $R$ and $S$ be represented by the matrices $M_R$ and $M_S$ respectively: $M_R = \left( \begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array} \right) \qquad M_S = \left( \begin{array}{cccc} 1 & 0 & 1 & 1 \\ 0 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 1 & 0 & 0 \end{array}\right)$
a) Is $R \subseteq S$ ?
b) Is $S \subseteq R$ ?
c) Write down the matrix for $R \cup S$ .
d) Write down the matrix for $R \cap S$ .
Can a relation be both reflexive and antireflexive? If so, give an example; if not, give an explanation.
Can a relation be both symmetric and antisymmetric? If so, give an example; if not, give an explanation.
(This problem assumes that you have already read Chapters 9-12.) Let $X$ be a set with $n$ elements. Count the number of:
a) reflexive relations on $X$ .
b) antireflexive relations on $X$ .
c) symmetric relations on $X$ .
d) antisymmetric relations on $X$ .
Verbally describe the matrix for a relation that is:
a) diagonal.
b) symmetric.
c) antireflexive.
d) antisymmetric.

16. Closure and composition

Let $X=\{a,b,c,d\}$ and the relation $R$ on $X$ be defined by $R = \{(a,b),(a,d),(b,d),(c,c)\}.$
a) Calculate the reflexive closure of $R$ .
b) Calculate the symmetric closure of $R$ .
c) Calculate the transitive closure of $R$ .
Let $Y=\{a,b,c,d,e\}$ and the relation $S$ on $Y$ be defined by $S = \{(a,b),(b,d),(c,d),(d,c),(d,e),(e,a)\}.$
a) Calculate the reflexive closure of $S$ .
b) Calculate the symmetric closure of $S$ .
c) Calculate the transitive closure of $S$ .
Consider the relation $R = \{(a,c),(b,a),(b,b),(c,f),(d,e),(e,d)\}$ on the set $X = \{a,b,c,d,e,f\}$ .
a) Calculate the reflexive closure of $R$ .
b) Calculate the symmetric closure of $R$ .
c) Calculate the transitive closure of $R$ .
Consider the relation $R$ on the set $\{x_1, x_2, x_3, x_4, x_5\}$ given by $R = \{(x_1,x_4), (x_2,x_4), (x_3,x_2), (x_3,x_3), (x_4,x_2), (x_4,x_5), (x_5,x_5)\}.$
a) What pairs must you add to $R$ to construct its reflexive closure?
b) What pairs must you add to $R$ to construct its symmetric closure?
c) What pairs must you add to $R$ to construct its transitive closure?
What is the reflexive closure of the relation described by $x < y$ on $\mathbf{R}$ ?
What is the symmetric closure of the relation described by $x < y$ on $\mathbf{R}$ ?
Let $R$ and $S$ be relations on $X = \{x_1, x_2, x_3\}$ represented by the matrices $M_R = \left[ \begin{array}{ccc} 1 & 0 & 1 \\ 0 & 0 & 1 \\ 1 & 1 & 0 \end{array} \right] \qquad M_S = \left[ \begin{array}{ccc} 0 & 0 & 0 \\ 1 & 1 & 0 \\ 1 & 0 & 1 \end{array}\right].$
a) Write down $RS$ as a set of ordered pairs.
b) Write down $SR$ as a set of ordered pairs.
Let $S = \{(a,b),(b,a),(b,d),(b,e),(b,f), (c,c),(d,e),(f,c),(f,f)\}$ be a relation on the set $\{a,b,c,d,e,f\}$ . Write the relation $S^2$ as a set of ordered pairs.
Let $X=\{x_1,x_2,x_3,x_4\}$ , $Y=\{y_1,y_2,y_3\}$ , and $Z=\{z_1,z_2\}$ . Let $R$ be the relation from $X$ to $Z$ with $R=\{(x_1,z_1),(x_2,z_2),(x_3,z_1),(x_3,z_2)\}$ . Let $S$ be the relation from $Y$ to $X$ where $S = \{(y_1,x_4),(y_1,x_1),(y_2,x_3),(y_3,x_2)\}$ .
a) Write down the matrices $M_R$ and $M_S$ . Order the rows and columns numerically.
b) Write down the composition $SR$ as a set of ordered pairs.
Why is there no such thing as an antireflexive closure?
Why is there no such thing as an antisymmetric closure, and why is this idea actually less useful than the idea of an antireflexive closure?

17. Equivalence relations

Let $X=\{a,b,c,d,e,f\}$ and $R$ be the relation on $X$ defined by $R = \{ (a,a), (a,b), (a,e),$ $(b,a), (b,b), (b,e),$ $(c,c), (c,f), (d,d),$ $(e,a), (e,b), (e,e),$ $(f,c), (f,f) \}$ . Is $R$ an equivalence relation? If so, draw a digraph and give the equivalence classes. If not, give an example showing why.
Let $X=\{a,b,c,d,e,f\}$ and $S$ be the relation on $X$ defined by $S = \{ (a,a), (a,b), (a,c),$ $(a,d), (a,e), (a,f),$ $(b,b), (b,d), (b,e),$ $(b,f), (c,c), (c,d),$ $(c,e), (c,f), (d,d),$ $(d,e), (d,f), (e,e), (f,f) \}.$ Is $S$ an equivalence relation? If so, draw a digraph and give the equivalence classes. If not, give an example showing why.
Let $X=\{a,b,c,d,e,f\}$ and $T$ be the relation on $X$ defined by $T = \{ (a,b), (a,c), (a,d),$ $(c,b), (c,d), (d,b),$ $(e,a), (e,b), (e,c),$ $(e,d), (e,f), (f,a),$ $(f,b), (f,c), (f,d) \}.$ Is $T$ an equivalence relation? If so, draw a digraph and give the equivalence classes. If not, give an example showing why.
Let $X$ be any finite set and define the relation $R$ on $\mathcal{P}(X)$ by
$R = \{ (E,F) \; | \; |E| = |F|, E, F \in \mathcal{P}(X) \}.$
a) Prove that $R$ is an equivalence relation.
b) If $X = \{a,b,c\}$ , give the equivalence classes of the relation.
Throughout this book we have used the notation $[n]$ as shorthand for the set $\{1, 2, \ldots, n\}$ . Now we are using $[x]$ to refer to the set of all elements equivalent to $x$ in a given equivalence relation. Briefly discuss the connection between the two notations, and why it is “okay” to use the same notation for these two things. (What is $[X]$ in the equivalence relation on a collection of sets described in the previous question?)
Let $\mathcal{S}^2$ be the space of all well-formed formulas consisting of at most two different letters. In other words, $\mathcal{S}^2$ is the set consisting of all statements correctly formed from $p$ , $q$ , and some logical connectives. Examples include $p$ , $p \wedge \neg q$ , and $(\neg p \vee \neg q) \to (p \wedge q)$ . Define the relation $\equiv$ on $\mathcal{S}^2$ by saying $\varphi \equiv \psi$ whenever $\varphi \leftrightarrow \psi$ is a tautology. (In other words, $\equiv$ on $\mathcal{S}^2$ is the familiar logical equivalence.)
a) Prove that $\equiv$ is an equivalence relation.
b) Prove there are 16 equivalence classes. (This requires you to have read Chapters 9-13.)
c) List the 16 equivalence classes.
Fix a nonzero integer $n$ . Prove that the relation on the integers defined by $a \equiv b \; (\text{mod } n)$ is an equivalence relation. (Hint: For transitivity, you will need to assume that if $a$ divides two numbers, it divides their sum as well. Though, this is worth proving on its own.)
Simplify each of the following (write the smallest non-negative member of the appropriate equivalence class).
a) $28 \; (\text{mod } 9)$
b) $(-50) \; (\text{mod } 23)$
c) $(-17) \; (\text{mod } 3)$
d) $(18 \times 321) \; (\text{mod } 4)$
e) $(7^2 - 300) \; (\text{mod } 4)$
f) $(302^5-97\times 108) \; (\text{mod } 5)$
g) $(7^{14} - 28 \times 20) \; (\text{mod } 6)$
Let $X$ be the set $\{0,1,2,3,4,5,6,7,8,9,10\}$ . Write down the equivalence relations of this set under the relation $\equiv\, (\text{mod } 3)$ .
Simplify $2^{27}\, (\text{mod } 5)$ by hand in the following way.
a) Express $2^{27}$ as a product of factors of the form $2^{2^n}$ by writing $27$ as a sum of powers of 2 (basically, in binary).
b) Use the arithmetic properties of the modulus function to simplify $2^{2^n}\, (\text{mod } 5)$ for each of the powers of 2 in the product you found in the preceding part. (Hint: Notice that each power of 2 is a square of the preceding part. So to simplify $2^{16}\, (\text{mod } 5)$ , you could simplify simplify $2^{8}\, (\text{mod } 5)$ , square that, and then take its remainder modulo 5.)
c) Multiply the remainders you found in the preceding part, taking one last remainder mod $5$ if necessary. (This method is used to simplify large numbers of the form $b^c \, (\text{mod } n)$ , which is used in certain encryption protocols.)

18. Partial orders

Let $X=\{a,b,c,d,e,f\}$ and $R$ be the relation on $X$ defined by $R = \{ (a,a), (a,b), (a,e),$ $(b,a), (b,b), (b,e),$ $(c,c), (c,f), (d,d),$ $(e,a), (e,b), (e,e),$ $(f,c), (f,f) \}$ . Is $R$ a partial order? If so, draw its Hasse diagram. If not, give an example showing why.
Let $X=\{a,b,c,d,e,f\}$ and $S$ be the relation on $X$ defined by $S = \{ (a,a), (a,b), (a,c),$ $(a,d), (a,e), (a,f),$ $(b,b), (b,d), (b,e),$ $(b,f), (c,c), (c,d),$ $(c,e), (c,f), (d,d),$ $(d,e), (d,f), (e,e), (f,f) \}$ . Is $S$ a partial order? If so, draw its Hasse diagram. If not, give an example showing why.
Let $X=\{a,b,c,d,e,f\}$ and $T$ be the relation on $X$ defined by $T = \{ (a,b), (a,c), (a,d),$ $(c,b), (c,d), (d,b),$ $(e,a), (e,b), (e,c),$ $(e,d), (e,f), (f,a),$ $(f,b), (f,c), (f,d) \}$ . Is $T$ a partial order? If so, draw its Hasse diagram. If not, give an example showing why.
Let $X$ be any set and define the relation $S$ on $\mathcal{P}(X)$ where $S = \{(E,F) \; | \; E \subseteq F \subseteq X\}.$
a) Prove that $S$ is a partial order.
b) Is $S$ a linear order? If not, tell why.
c) Give the maximal and minimal elements of $S$ .
d) If $X=\{a,b,c,d\}$ , draw the Hasse diagram for $S$ .
Let $\mathcal{B}_2$ be the set of all $2\times 2$ Boolean matrices, and let $T$ be the relation on $\mathcal{B}_2$ where $T = \{(A,B)\;|\; A \le B, A, B \in \mathcal{B}_2 \}.$
a) Prove $T$ is a partial order on $\mathcal{B}_2$ (hence justifying the use of the symbol $\le$ for Boolean matrices).
b) Is $T$ a linear order? If not, tell why.
c) Give the maximal and minimal elements of $T$ .
d) Draw the Hasse diagram for $T$ .
It sure seems like this should be a partial order: take a family of sets, and declare $E$ to be related to $F$ if $|E| \le |F|$ . Why isn’t it? Provide a specific example using two sets.
Let $\mathcal{A}$ be a Boolean algebra; again, that is a set equipped with elements $0$ and $1$ and operations $\vee$ , $\wedge$ , and $\neg$ , following the appropriate distributive laws (see Chapter 14) where $a \wedge 0 = 0$ and $a \vee 1 = 1$ for all $a \in \mathcal{A}$ . Define a partial order $\le$ on $\mathcal{A}$ by saying $a \le b$ if and only if $a \vee b = b$ .
a) Prove that $\le$ is indeed a partial order.
b) Prove that, in fact, $\mathcal{A}$ forms a lattice under $\le$ .
c) Pick two of the preceding problems you could have skipped by doing this question first. (It is good practice to work out both concrete examples of things and then general situation.)
The Hasse diagram for the partial order $R$ is shown.

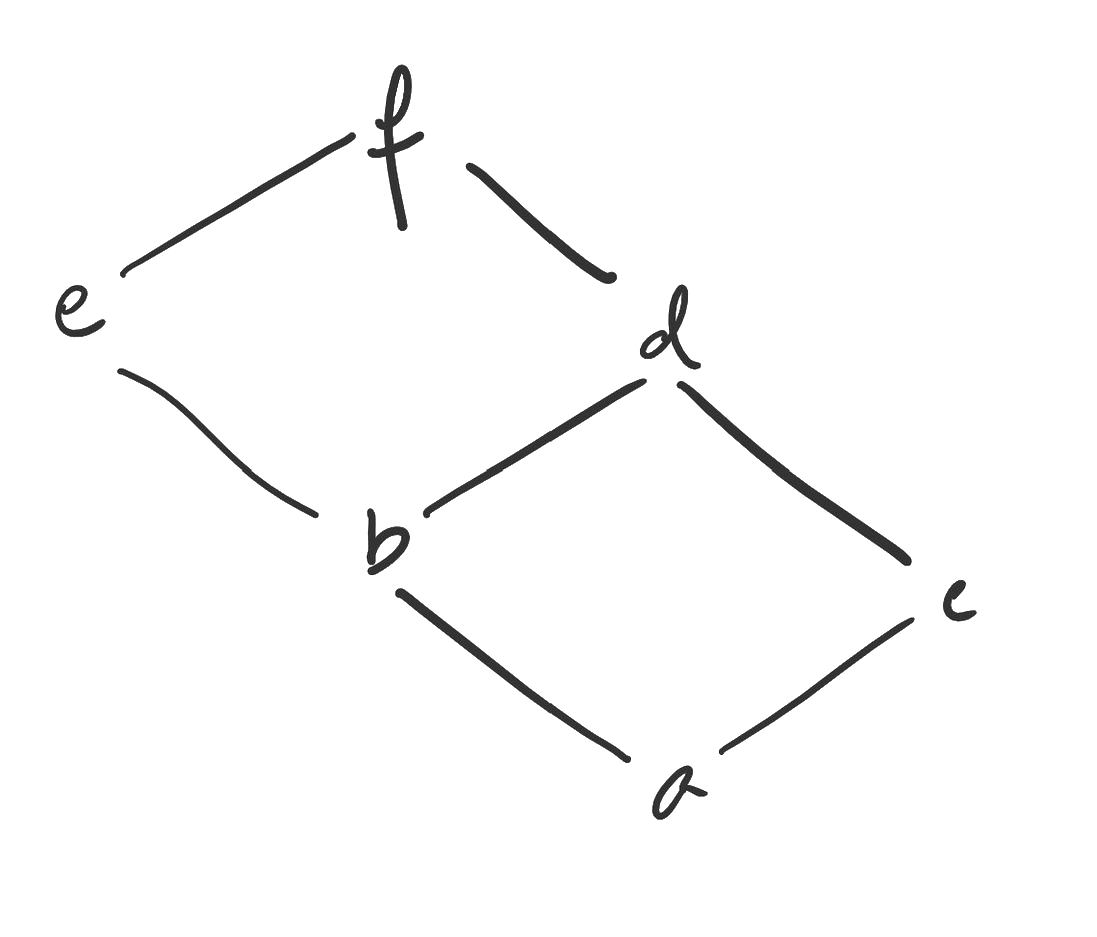
Figure. The Hasse diagram for a partial order where a is related to b and c, b is related to e and d, c is related to d, and e and d are related to f.

a) Give the lower bounds of the set $\{a,b,c\}$ .
b) Give the greatest lower bound of the set $\{a,b,c\}$ .
c) Give the upper bounds of the set $\{a,b,c\}$ .
d) Give the least upper bound of the set $\{a,b,c\}$ .
e) Does the partially ordered set shown form a lattice?
f) What are the maximal elements of the partial order?
g) Is there a maximum?
h) What are the minimal elements of the partial order?
i) Is there a minimum?
The Hasse diagram for the partial order $S$ is shown.

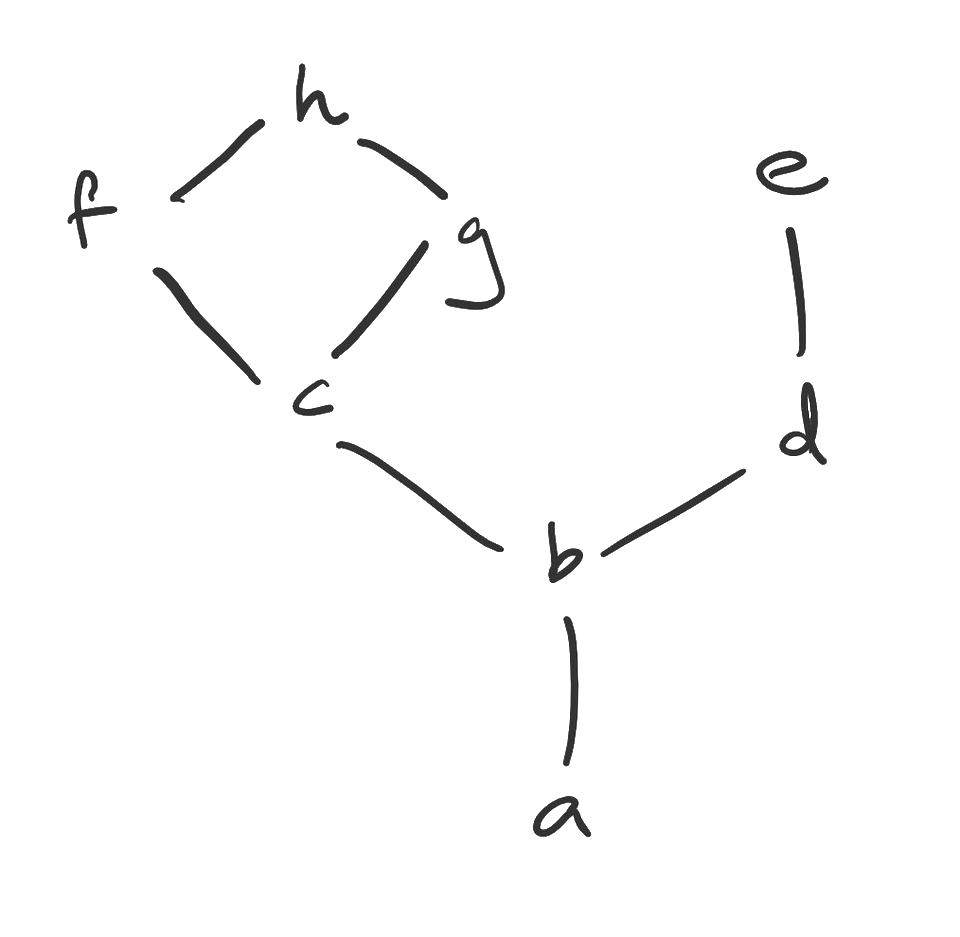
Figure. The Hasse diagram for a partial order where a is related to b, b is related to c and d, d is related to e, c is related to f and g, and f and g are both related to h.

a) Give the lower bounds of the set $\{b,c,d\}$ .
b) Give the greatest lower bound of the set $\{b,c,d\}$ .
c) Give the upper bounds of the set $\{b,c,d\}$ .
d) Give the least upper bound of the set $\{b,c,d\}$ .
e) Does the partially ordered set shown form a lattice?
f) What are the maximal elements of the partial order?
g) Is there a maximum?
h) What are the minimal elements of the partial order?
i) Is there a minimum?
The Hasse diagram for the partial order $T$ is shown.

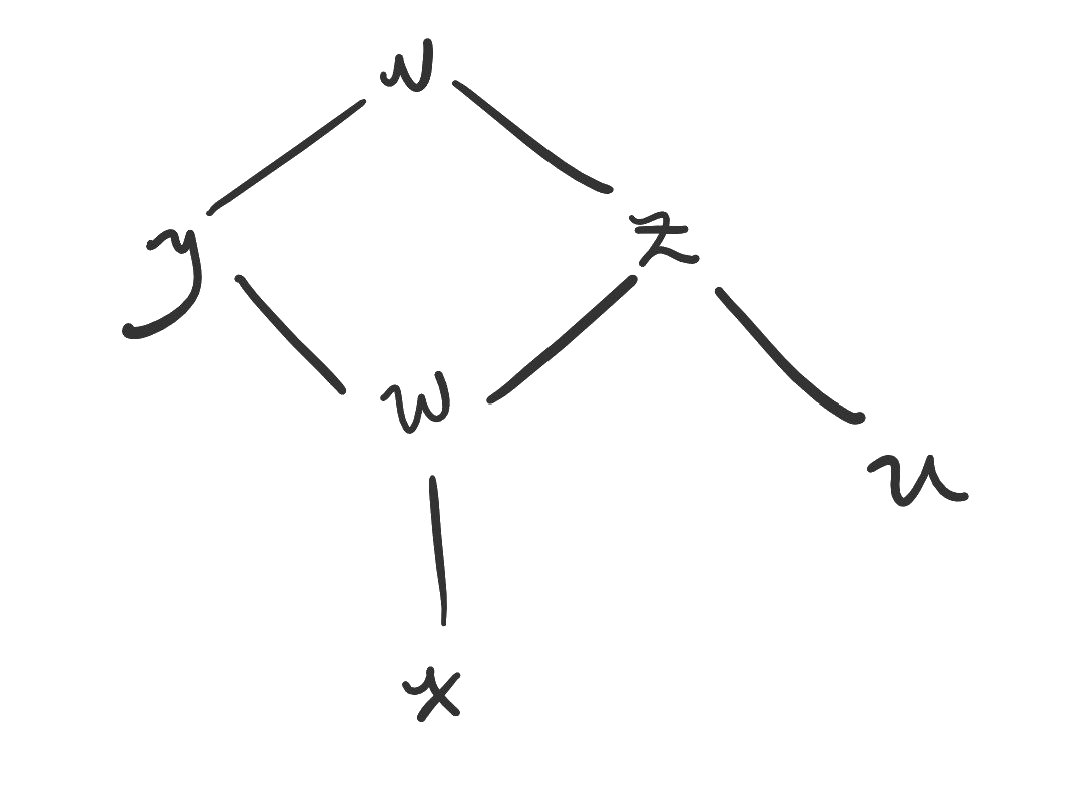
Figure. The Hasse diagram for a partial order where x is related to w, w is related to y and z, u is related to z, and both y and z are related to v.

a) Is $T$ linear?
b) What are the minimal elements in $T$ ? Is there a minimum? If so, what is it?
c) What are the maximal elements in $T$ ? Is there a maximum? If so, what is it?
d) Let $A$ be the set $\{v,y,z\}$ . What are the lower bounds of $A$ , if any? What is $\text{glb}(A)$ , if it exists?
e) What are the upper bounds of $A$ , if any? What is $\text{lub}(A)$ , if it exists?
f) Let $B$ be the set $\{u,w,z\}$ . What are the lower bounds of $B$ , if any? What is $\text{glb}(B)$ , if it exists?
g) What are the upper bounds of $B$ , if any? What is $\text{lub}(B)$ , if it exists?
h) Write the set of ordered pairs in $T$ .
i) What is the largest lattice contained in $T$ ? (i.e., Choose a subset of the underlying set such that the order restricted to that subset creates a lattice. In this case, this operation should give a unique result.)
j) What is the smallest lattice containing $T$ ? (i.e. Add arrows to the relation such that the result is a lattice. In this case, this operation should give a unique result.)